Question
If (a + b) = 1 and (1/a) – 2b = 5/a then find the
value of a2 + b2.Solution
As, a2 + b2 = (a + b)2 – 2ab ------------- (1) (1/a) – 2b = 5/a 1/a – 5/a = 2b - 4/a = 2b 2ab = - 4 Substitute the values of 2ab and a + b in (1) a2 + b2 = 1 - (-4) = 5
A great reformer of the 19th century India, he fought for the conditions of women and the lower castes and was himself subjected to child marriage. He ...
What is the name of the oil painting by Amrita Sher-Gil, created in 1937, depicting village women engaged in daily activities?
Which political party established the Second Backward Classes Commission in 1978?
According to Mahatma Gandhi's 'Hind Swaraj' (1909), British rule in India was established _____.
Consider the following statements:
1. The teachings of Ramkrishna Paramhansa are characterized by the real-life issues of a common man.
Which ruler of the Mauryan Empire constructed the Sanchi Stupa?
Who was the first Governor-General of independent India?
Consider the following pairs in the context of Anglo-Maratha wars:
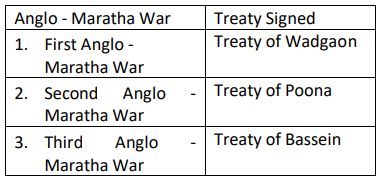
Consider the following statements with reference to the Subsidiary alliance system:
1. Indian rulers had to accept a permanent stationing of th...
In the context of Indian history, what was the Dandi March
Relevant for Exams:



