Continue with your mobile number
x + y + xy = 118
Add 1 on both sides of the equation, we get,
1 + x + y + xy = 118 + 1
Or, (1 + x) + y X (1 + x) = 119
So, (1 + x) X (1 + y) = (7 X 17) or (1 X 119)
When, (1 + x) X (1 + y) = 7 X 17
We can say that, 1 + x = 17 or 1 + y = 17
So, 1 + x = 17 or, 1 + y = 17
So, x = 16 or y = 16
When, x = 16, y = 6 and when y = 16, x = 6
So, for both cases, x + y = 16 + 6 = 22
Glufosinate inhibits the enzyme
Food Analysts have a major role to play in ______ of food samples in the food laboratories
For hybrid seed production_______ flowers are completely suppressed on female plants.
Ufra disease in rice is caused by ___
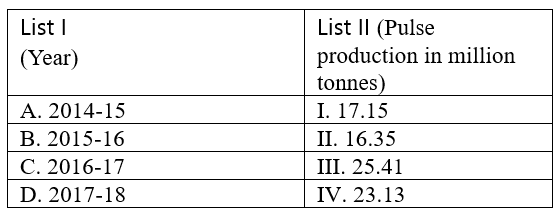
Match List I with List II
Which insects do not belong to the order Diptera?
Aflatoxin, a mycotoxin produced by Aspergillus, is associated with ____ crop.
The following is not included under purpose wise classification of credit
For how much time period we can store food grain in rural godown?
In which condition roller is used: