Question
Solution
(m - 4) 2 + (n + 5) 2 + (p - 3) 2 = 0, then find the value of 2m + 3n - p.
If x + y + z = 6, and x3 + y3 + z3 = 36, xyz = 6 then find (xy +yz + zx)?
(x – 4)2 + (y + 3) 2 + (z – 5) 2 = 0, then find the value of 2x + 3y – z.
The roots of the quadratic equation x² + px + q = 0 are in the ratio 3:4. If the sum and product of the roots are 7 and 12, respectively, find the valu...
If the length of a rectangle is increased by 40%, and the breadth is decreased by 20%,then the area of the rectangle increases by x%. Then the value of ...
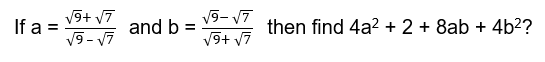
If 1/(x+ 1/(y+ 1/z)) = 13/30, then find x+y+z= ?
What is the HCF of (x³ + 3x² - x - 3) and (x³ + 4x² + x - 6)?
Length of each side of a rhombus is 13 cm and one of the diagonal is 24 cm. What is the area (in cm2) of the rhombus?
The length of a rectangle is four times its breadth. If its length is increased by 20 cm and breadth is increased by 20 cm, the area of the rectangle is...



