Question
A boat can cover 90 km upstream and 225 km downstream in
15 hours. Speed of the stream is how much less than the speed of the boat in still water if the boat can cover 72 km upstream and 180 km downstream in 12 hours?Solution
ATQ, Let the upstream speed and downstream speed of the boat be x km/h and y km/h, respectively. So according to question: 90/x + 225/y = 15 ………………. (i) Also, 72/x + 180/y = 12 ……….. (ii) Solving (i) and (ii), we get x = 18 and y = 36 So, the upstream speed and downstream speed of the boat are 18 km/h and 36 km/h, respectively. Speed of the boat in still water = (18 + 36)/2 = 27 km/h Speed of the stream = (36 – 18)/2 = 9 km/h So, the desired difference = 27 – 9 = 18 km/h
In a class, all the students are standing in a row. If a particular student is 18th from both the ends, how many students are there in the cl...
If the sum of runs scored by M and N is 88 and the sum of runs scored by N and P is 66, then what is the probable number of runs scored by L?
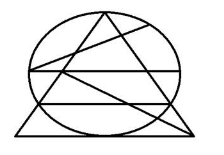
Find the number of triangles in the given figure:
A is more intelligent than B, B isn’t as intelligent as C. C is more intelligent than D but not as good as A. Who’s the most intelligent of them all...
Five people K, L, M, N, and Z read newspaper the person who read it first give it to M. The person who read it last took it from K. Z was neither first ...
Answer the questions based on the information given below.
Nine persons F, G, H, I, J, K, L, M and N are ranked according to their height. At l...
In a queue of 90 people, Ms. Braganza is 23rd from the right and Ms. Margaret is 28th from the left. How many people are there between Ms. Braganza and ...
Select the option that is related to the third number in the same way as the second number is related to the first number.
13 : 2366 :: 10 : ?...
In a certain code language, "BOND" is coded as 24 and "PLANT" is coded as 67. How will "SMART" be coded in that language?
In a row of girls Sangeeta is 8th from the right and Kamla is 20th from the left. When Sangeeta and Kamla Interchange position, Ka...
Relevant for Exams:


