Question
In the given diagram, point 'O' represents the center of
a circle, while AB and DE are two distinct chords within the circle. The line segment OC is perpendicular to the chord AB, and the segment OF is perpendicular to the chord DE. The length of chord AB is provided as 24 cm, and the distance CF from the center to the perpendicular intersection with chord DE is (5 + 4√5) cm. The radius of the circle measures 13 cm. Determine the length of chord DE.Solution
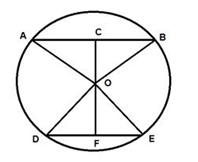 The perpendicular from the centre of the circle to its chord, bisects the chord. So, AC = CB = (24/2) = 12 cm Similarly, DF = FE In right rAOC, using Pythagoras theorem, AO2 = AC2 + CO2 Or, 132 = 122 + CO2 So, CO2 = 169 - 144 = 25 Or, CO = √25 = 5 cm And, OF = CF - CO = 5 + 4√5 - 5 = 4√5 cm In right rDOF, using Pythagoras theorem, DO2 = DF2 + OF2 So, DF2 = 132 - (4√5)2 Or, DF2 = 169 - 80 = 89 So, DF = √89 cm DE = DF + FE = 2DF = 2√89 cm
The perpendicular from the centre of the circle to its chord, bisects the chord. So, AC = CB = (24/2) = 12 cm Similarly, DF = FE In right rAOC, using Pythagoras theorem, AO2 = AC2 + CO2 Or, 132 = 122 + CO2 So, CO2 = 169 - 144 = 25 Or, CO = √25 = 5 cm And, OF = CF - CO = 5 + 4√5 - 5 = 4√5 cm In right rDOF, using Pythagoras theorem, DO2 = DF2 + OF2 So, DF2 = 132 - (4√5)2 Or, DF2 = 169 - 80 = 89 So, DF = √89 cm DE = DF + FE = 2DF = 2√89 cm
Find the missing number.
.
...Choose the correct alternative that will complete the given number series. 2, 9, 28, 65, ?, 217
In the following question, select the missing number from the given alternatives.
45, 15, 60, 75, 135, ?
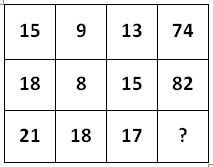
Study the given pattern carefully and select the number that can replace the question mark [?] in it.
Study the given pattern carefully and select the number that can replace the question mark [?] in it.
First row: 6, 5, 191
Second row: 9, ...
Select the number that can replace the question mark (?) in the following series.
Select the number from the given option that can replace the question mark (?) in the following series:
32, 16, 24, 60, ?, 945
Find the missing term :
...
Select the missing number from the given responses.
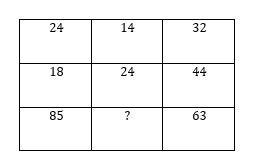
Find the missing term in the given series:
4 3.5 ? 22.875 ...


