Question
What is the value of (4ab+ab2)/(a2
b), a,b ≠0 I. a + b = 0 II. a – b = 1 Each of the following questions below consists of a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements are sufficient to answer the question. Read both the statements and give the answer.Solution
(4ab+ab2)/(a2 b)= (4+b)/a From I, we get a = -b And from II, we get a = 1 + b Putting the values of ‘a’ in the above equation and equating both (4+b)/a = (4+b)/(-b) Also, (4+b)/a= (4+b)/(1+b) = (4+b)/(-b) b = -1/2 a = 1/2 (4ab+ab2)/(a2 b)= (4(-1/4)+1/2 x (-1/2)2)/((1/2)2 (-1/2))= (-1+1/8)/(-1/8)=7
sin2 9 ° + sin2 10 ° + sin2 11 ° + sin2 12 ° + ……… + sin2 81 ° = ?
...A 16-meter-long rope is stretched from the ground to the top of a house, forming a 30° angle with the ground. Determine the height of the house.
What is the value of cos [(180 – θ)/2] cos [(180 – 9θ)/2] + sin [(180 – 3θ)/2] sin [(180 – 13θ)/2]?
If θ is an acute angle and sin θ + cosec θ = 2, then the value of sin2 θ + cosec2 θ is:
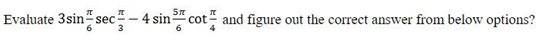
If Sin θ + Cos θ = √2 Cos(90 - θ ), then find the value of Cot θ ?
...If tan A = 4/3, 0 ≤ A ≤ 90°, then find the value of sec A.
[(sinx – 2sin 3 x)/(2cos 3 x – cosx)] 2 + 1, x ≠45 o , is equal to:
Relevant for Exams:



