New 55% Off on All Courses - Enroll Now! Click Here

    Question

    Answer the following questions based on the data provided:   A merchant conducts business with four different articles, labelled as 'A,' 'B,' 'C,' and 'D.' The table below displays the marked price for each article, the percentage of discount offered on each article, and the profit (in Rs.) earned from selling each article, expressed as a percentage of the discount offered on the same article:   Additional information:   => Profit earned on selling article 'A' is Rs. 50 less than that on article 'D'   => 2x – y/2 = 90   => 3y – x/2 = 35  

    Find the ratio of average of selling price of each unit

    of articles 'B' and 'C' together to cost price of each unit of article 'A'
    A 11:4 Correct Answer Incorrect Answer
    B 15:4 Correct Answer Incorrect Answer
    C 19:4 Correct Answer Incorrect Answer
    D 15:17 Correct Answer Incorrect Answer
    E 15:7 Correct Answer Incorrect Answer

    Solution

    Given,   2x – y/2 = 90   Or, 4x - y = 180 ....... (I)   And, 3y – x/2 = 35   Or, (6y - x) = 70 ........ (II)   On adding equation (I) with 4 × equation (II), we have;   4x + (-4x) - y + (24y) = 180 + 70 X 4   Or, 23y = 460   So, y = 20   So, 4x = 180 + 20 ..... (From equation I)   Or, x = 200 ÷ 4 = 50   So, marked price of article 'A' = 4 × 50 = Rs. 200   And, percentage discount offered on article 'A' = 1.25y% = 1.25 × 20% = 25%   So, discount offered = 200 × 0.25 = Rs. 50   So, profit earned on article 'A' = 50 × 1.4 = Rs. 70   So, profit earned on article 'D' = 70 + 50 = Rs. 120   Marked price of article 'D' = Rs. 400   Percentage discount offered = 2y% = 2 × 20 = 40%   So, discount offered = 400 × 0.4 = Rs. 160   ATQ;   (120/160) × 100 = {z - (x/2)}   Or, 75 = z - 25   So, z = 100   For article 'A':   Marked price of the article = Rs. 200   Discount offered = Rs. 50   Selling price = 200 - 50 = Rs. 150   Profit earned = Rs. 70   So, cost price = 150 - 70 = Rs. 80 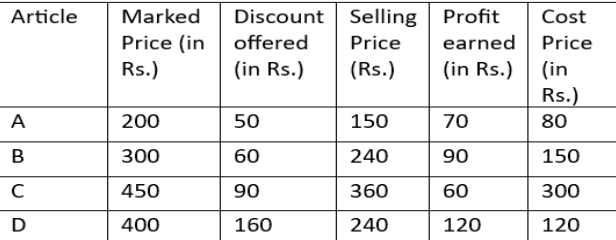  Average selling price of articles 'B' and 'C' together = (240 + 360) ÷ 2 = Rs. 300   Cost price of article 'A' = Rs. 80   So, required ratio = 300:80 = 15:4  

    Practice Next

    Relevant for Exams: