Question
In an 800-meter race involving 'Amit', 'Bhanu', and
'Chinky', calculate the distance 'Amit' was ahead of 'Chinky'. Statement I : 'Amit' finishes 160 meters ahead of 'Bhanu'. Statement II: The speed of 'Bhanu' compared to 'Chinky' is in the ratio of 8:9. The question includes two statements, labeled "I and II." You must determine if the information in these statements is enough to figure out the question asked.Solution
ATQ, We know that when time is constant, ratio of distance covered = ratio of speed Statement I: Ratio of distance covered by 'Amit' and 'Bhanu' = 800:(800 - 160) = 800:640 = 5:4 So, data in statement I alone is not sufficient to answer the question. Statement II: Ratio of speeds of 'Bhanu' and 'Chinky' = 8:9 So, data in statement II alone is not sufficient to answer the question. On combining both statements, we have; Ratio of speeds of 'Amit' and 'Bhanu' = 5:4 And ratio of speeds of 'Bhanu' and 'Chinky' = 8:9 So, ratio of speeds of 'Amit', 'Bhanu' and 'Chinky' = 10:8:9 So, distance covered by 'Chinky' in the time taken by 'Amit' to cover 800 metres = 800 × (9/10) = 720 metres So, 'Amit' beat 'Chinky' by 800 - 720 = 80 metres So, the data in both statements I and II together is necessary to answer the question.


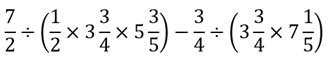
/Quantitative_Aptitude/Simplification/233429_590713.gif)
