Question
Which of the following pairs of non-zero values of p and
q make 6-digit number 674pq0 divisible by both 3 and 11?Solution
Given that 674pq0 is divisible by 3 and 11 For this question we will use divisibility rule 3 divisibility rule = sum of digits should be divisible by 3. 11 divisibility rule = sum of even places - sum of odd places = 0 ,11,22,33...... Here we have , 674pq0 According to divisibility rule of 3 => 6+7+4+p+q+0 = 17+p+q => it should be multiple of 3 So, the possible value of p+q = 1 , 4 , 7, 10, 13..... Now you can see the option or you can apply 11 rule as well. Then from the option only option 2 and 3 are satisfying the condition that sum should be 1,4,7..... but option 2 is not satisfying the divisibility rule of 11 . So option 2 can not be the answer of this question . Option 3 which is p = 5 and q =2 is satisfying both the rules of 3 and 11.
The "History of British India" is a three-volume work by ________.
Consider the following statements with reference to the steps taken by Britishers post revolt of 1857:
1. The number of Indian soldiers increas...
In the 2024 Best Countries ranking, which country topped the “Best Countries for Adventure” list?
Which movement was launched by Mahatma Gandhi in 1942.
Which of the following statements regarding Indian Factory Act, 1891 is/are correct?
1. It increased the minimum and maximum age limit for chi...
The Jallianwala Bagh massacre took place in which year?
The 'Rashtriya Swayamsevak Sangh' (RSS) was founded in which year?
With reference to the Civil Disobedience Movement, consider the following statements
1. India’s First Civil Disobedience Movement was carried o...
Which among the following relates to caste movement in India?
1. Ezhava movement.
2. Nadar movement.
3. Mahar Movement.
...Match the following lists:
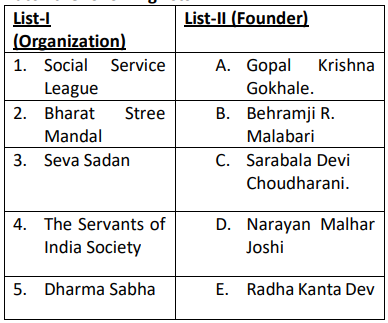
Select the correct answer f...
Relevant for Exams:


