Question
Consider two concentric circles having radii 17 cm and
15 cm. What is the length (in cm) of the chord, of the bigger circle, which is a tangent to the smaller circle?Solution
Given:  Radius of circles r1= 15 cm  r2= 17 cm Property of tangent - A tangent is perpendicular to the center of the circle. Property of chord - A perpendicular line drawn from the center of the circle to the chord of the circle always divide the chord in half.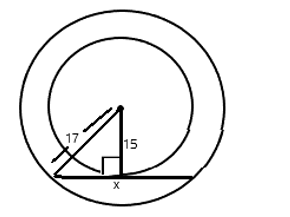 
Applying the property of chord and tangent: We find that- 172 = 152+(x/2)2 289 = 225 +x2 /4 289 – 225 =x2 /4 x2 =256 x=16  Therefore, length of the chord = 16 cm.
In blood, platelets are required for
Which of the following statements is/are correct?
1. Amnion contains fluid.
2. Ultrasound scan can detect the sex of an embryo.
Sel...
Two wires of identical radius of cross-section rrr, but made of different materials, are joined end-to-end (i.e., in series). If the number density of f...
What is the process of changing a substance directly from solid to gas called ?
Which gas is most abundant in Earth's atmosphere?
A liquid rises in a capillary tube due to:
Which of the following is used as red pigment in making batteries, lead glass and rust proof primer paints?
Which of the following materials is a good insulator?
What happens when light enters a glass slab from air?
When the heavier component in a mixture settles after water is added to it, the process is called _______.
Relevant for Exams:
