Question
If in the given figure AD is perpendicular to BC, AC =
26 units, CD = 10 units, BC = 42 units, triangle DAC whose angle is x and angle B = y, then, find the value of 6/cosx -5/cosy +8 tany =?Solution
In ∆ ADC – AD = √(AC)2-DC2 ) AD = √(262-102 ) AD = √(676-100) AD = √576 = 24 AD = 24 Now in ∆ABD AB = √(AD)2+(BD)2 ) AB = √(242+322 AB = √(576+1024) = √1600 AB = 40 NOW- ∴The side opposite to the angle is the hypotenuse, so the base for angle x will be AD. cosx=24/26 cosy=32/40 tany=24/32 6/cosx -5/cosy +8 tany =? =6/(24/26)-5/(32/40)+8×24/32 =26/4 - 25/4 + 24/4 =(50-25)/4 =25/4 6/cosx -5/cosy +8 tany =25/4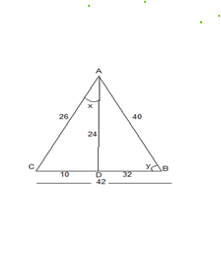
In a structured database, which data storage format would best support hierarchical data with varying levels of nested attributes?
Which of the following semantic HTML tags is best suited for defining a block of navigation links?
Which of the following best describes the role of data analysis in credit scoring within the finance industry?
In descriptive statistics, which of the following measures is least affected by extreme values (outliers)?
Which data transformation scales features to a range of 0 to 1?
In hypothesis testing, what does a p-value less than 0.05 typically indicate?
Which type of machine learning technique is best suited for supervised learning tasks?
Which of the following is the primary purpose of exploratory data analysis (EDA)?
Which of the following best represents semi-structured data?
A data analyst is tasked with forecasting quarterly sales for the upcoming year based on the last five years of sales data. Which of the following metho...


