Question
Two ships are on opposite sides in front of a lighthouse
in such a way that all three of them are in line. The angles of depression of two ships from the top of a lighthouse are 30° and 60°. If the distance between the ships is 230√3  m, then find the height (in m) of the lighthouse.Solution
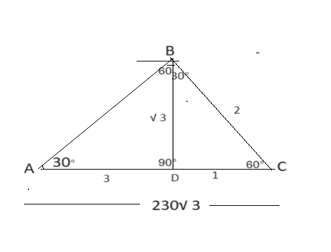Let the length of the lighthouse = BD m Use this property - When the angles of a triangle are 30 ° ,60 ° , and 90° respectively, the ratio of the opposite sides is 1: √ 3:2. When Triangle BDC – The opposite side of angle 30° = 1 Similarly - angle 60° =     √ 3, and angle 90° =2 Triangle ABD -opposite side of angle 30 ° =BD = 1= √ 3……. means √ 3times. so -opposite side of angle60° =AD = √ 3 = √ 3× √ 3 =3 now – AD + DC = AC 4= 230 √ 3 1= (230 √ 3)/4 Now height = BD = √ 3= (230 √ 3/4) × √ 3= (230 ×3)/4 =690/4 =172.5meter
The two buildings are 100m apart. From the top of the first building, which is 60m tall, the angle of depression to the top of the second building is 45...
From the top of a straight pillar 20 meters high, the angle of elevation of the top of a straight tower was 45°. If the tower was 70 meters high, then ...
There is a 12 m tall hoarding pole on the top of a building. A person at some distance from the building, observes that the angle of elevation to the to...
A tree of height 'h' meters is partially bent at a certain point above the ground, causing its top to touch the ground at a distance of 12 meters from i...
Find the angle of elevation of a 125 √ 3m tower's top from a point 125 m away from its base.
A pole got broken by the wind whose top meets the ground at an angle of 30° at a distance of 45 meters from the foot. What was the total height of t...
The angle of elevation of the top of a building from a point on the ground is 30° and moving 40 meters towards the building it becomes 60°. The ...
The angle of depression of a point on the ground as seen from the top of a tower, 35 feet high, is 45°. Find the distance of the point on the ground fr...
A pole 21 m high casts a shadow 7√3 m long on the ground. Find the angle of elevation
Now a chord of a circle is such that AB = 10 cm. If the diameter of the circle is 20 cm, then the angle subtended by the chord at the center is.
