Question
A tree of height 'h' meters is partially bent at a
certain point above the ground, causing its top to touch the ground at a distance of 12 meters from its base. The bent portion forms a 45° angle with the ground. Determine the value of 'h'.Solution
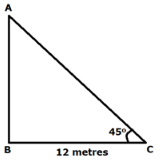Let the point from which the tree was bent be 'A'.In right triangle ABC, we havetan 45o = (AB/BC)So, AB = BC = 12 metresUsing Pythagoras theorem,AC2 = AB2 + BC2Or, AC2 = 122 + 122 = 144 + 144 = 288Or, AC = 12√2 metres (Since, height cannot be negative therefore, we will take positive root only)Length of the tree = h = (12√2 + 12) metres
The headquarter of State Bank of India is located at:
The ______ Schedule to the Constitution of India defines and specifies allocation of powers and functions between Union & States.
Who is the current Administrator of Chandigarh?
In which year India became a part of the Mineral Security Partnership (MSP), which is led by the USA?
The concept of 'Freedom of Press' is protected under which article of the Indian Constitution?
Cleanest river in the world is ?
Who invented the light bulb?
राजस्थान उत्पादन में देष में प्रथम है ?
From the invisible part of Sunlight, the process of photosynthesis is performed by:
Which of the following is a famous rock-cut temple complex located in the state of Himachal Pradesh?
Relevant for Exams:
