Question
The angle of elevation of a tower from a certain point of bus stand is 30°. When a man walks 5m ahead in the direction of the tower, the angle of elevation becomes 60°. What is the height of the tower?
Solution
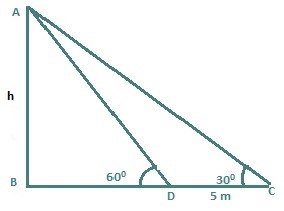Let, the height of the post = AB = ‘h’ m From ΔACB, ∠ACB = 30° [∵ given] tan ∠ACB = perpendicular/base ⇒ tan 30° = AB/BC ⇒ 1/√3 = h/BC ⇒ BC = h√3 ... (1) From ΔADB, ∠ADB = 60° [∵ given] tan ∠ADB = perpendicular/base ⇒ tan 60° = AB/BD ⇒ √3 = h/BD ⇒ BD = h/√3 ... (2) According to the question: BC - BD = 5 ⇒ h√3 - h/√3 = 5 ⇒ 2h/√3 = 5 ⇒ h = (5√3)/2 m
More Height and Distance Questions
- At a point 20 metres away from the base of a 20√3, metres high house, the angle of elevation of the top is
- The angle of depression of a point on the ground as seen from the top of a tower, 35 feet high, is 45°. Find the distance of the point on the ground from t...
- The angle of elevation of the top of a building from a point on the ground is 30° and moving 40 meters towards the building it becomes 60°. The hei...
- A shadow of a tower standing on level ground is found to be 40√3 meters longer when the Sun's altitude is 30° than when it is 60°. The height of the tower ...
- Two men are on opposite sides of a tower of 75 m height. If they measure the elevation of the top of the tower as 30deg; and 45deg; respectively then the d...
- A tree of height 'h' meters is partially bent at a certain point above the ground, causing its top to touch the ground at a distance of 12 meters from its ...
- A man 1.5 m tall is 22.5 m away from a tower 24 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.
- A tree breaks due to a storm and the top touches the ground 30 meters away from its base, making a 30-degree angle with the ground. What was the height of ...
- The two buildings are 100m apart. From the top of the first building, which is 60m tall, the angle of depression to the top of the second building is 45 de...
- From a point on the ground, the angle of elevation of the top of a tower is 45°. On walking 20 m towards the tower, the angle of elevation becomes 60°. Fin...
Relevant for Exams:
