Question
There is a 12 m tall hoarding pole on the top of a
building. A person at some distance from the building, observes that the angle of elevation to the top of the hoarding pole from that point is the same as the angle of elevation to the bottom of the hoarding pole if he moves 4 √ 3 m closer to the building. What is the angle of elevation that the person is seeing?Solution
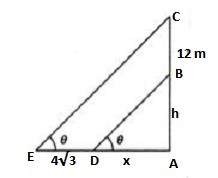Let AB be the building of height ‘h’ and BC be the hoarding pole of height 12 m. Let θ be the angle of elevation as seen by the person at a distance of ‘x’ m and ‘x + 4 √ 3‘ m. In Δ DAB, tan θ = h/x (i) In Δ EAC, tan θ = (h + 12)/ (x + 4 √ 3) (ii) From (i) and (ii) h/x = (h + 12)/ (x + 4 √ 3) ⇒ hx + 4 √ 3h = hx +12x ⇒ h/x = 12/ 4 √ 3 = √ 3 ⇒ tan θ = h/x = √ 3 = tan 60° ⇒ θ = 60°
Lichens, the pioneer organisms that initiate ecological succession are actually a symbiotic association of
Which one of the following is variety of triticale
‘The law of limiting factors’ was proposed by
In rust cycle, wheat is infected by which of the following spores?
Winter wheat is grown in
Movement of leaves of sensitive plant, Mimosa pudica are due to
Damping off and leaf blights are very effectively checked by
Seed plot technique of potato is used to produce
Breeder is having tag color of
Application developed by Indian institute of wheat and barley research for pest management in wheat crop is
Relevant for Exams:
