Question
There are two houses of the same height on both sides of
a 15-meter wide road. From a point on the road, elevation angles of the houses are 30° and 60° respectively. Find the height of the houses.Solution
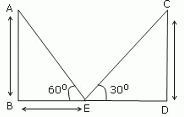Let y be the height of the houses, here AB = CD = y meter. Let x be the distance between the point on the road and the house making an elevation angle of 60°, here BE = x meter. Then, (15 - x) is the distance between the point on the road from the house making an elevation angle 30°, here DE = (15 - x) meter. Now, tan 60° = AB/BE ⇒ √3 = y/x ⇒ x = y/√3 ...(i) Also, tan 30° = CD/DE ⇒ 1/√3 = y/(15 - x) ⇒ √3y = 15 - x ⇒ √3y = 15 - y/√3 [from equation i] ⇒ 3y = 15√3 - y ⇒ 4y = 15√3 ⇒ y = 15√3/4 ≈ 6.5 meter
Which design pattern is most suitable for controlling access to a resource by limiting the number of clients that can use it concurrently?
The time complexity of binary search is:
In a binary tree, what is the maximum number of children a node can have?
Which type of AI is primarily used for adaptive mobile applications like virtual assistants?
Which of the following techniques is primarily used to address overfitting in machine learning models?
A data analysis algorithm requires processing data in a Last-In, First-Out (LIFO) manner. Which operation is used to get the most recently added element...
What type of relationship is represented by Aggregation in Object-Oriented Programming?
Consider the following sequence of stack operations:
PUSH(10) → PUSH(20) → PUSH(30) → POP() → PUSH(40) → POP() → POP()
What is...
Which of the following is true about triggers in a relational database?
Union-Find with path compression achieves nearly constant time because its complexity is:
Relevant for Exams:
