Question
There are two houses of the same height on both sides of
a 30-meter wide road. From a point on the road, elevation angles of the houses are 30° and 60° respectively. Find the height of the houses.Solution
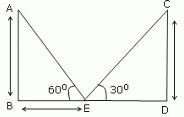Let y be the height of the houses, here AB = CD = y meter. Let x be the distance between the point on the road and the house making an elevation angle of 60°, here BE = x meter. Then, (30 - x) is the distance between the point on the road from the house making an elevation angle 30°, here DE = (30 - x) meter. Now, tan 60° = AB/BE ⇒ √3 = y/x ⇒ x = y/√3 ...(i) Also, tan 30° = CD/DE ⇒ 1/√3 = y/(30 - x) ⇒ √3y = 30 - x ⇒ √3y = 30 - y/√3 [from equation i] ⇒ 3y = 30√3 - y ⇒ 4y = 30√3 ⇒ y = 30√3/4 ≈ 12.9 meter
Under RBI’s guidelines, what is the maximum collateral-free loan amount permitted to startups for PSL classification?
Under which section of the Income Tax Act, 1961, is the term "person" defined?
Auditing begins where ______ ends.
The Article of a company may be altered by _____________
A person shall be eligible for appointment as an auditor of a company only if he is a _______________
The Udyam Registration Certificate can be obtained by which types of business entities?
In amalgamation in the nature of merger, which method is used?
Which of the following statements are true or false?
(i) Direct material cost: Cost of the material that can be directly allocated to a cost cent...
The delivery of goods by one person to another for some purpose, upon a contract that they shall, when the purpose is accomplished, be returned or other...
Under the Expected Credit Loss (ECL) model, how are trade receivables without a significant financing component measured for impairment?
Relevant for Exams:
