Question
Find the area of maximum side of square that can be
inscribed in a right angled triangle of side 15, 20 and 25 cm.Solution
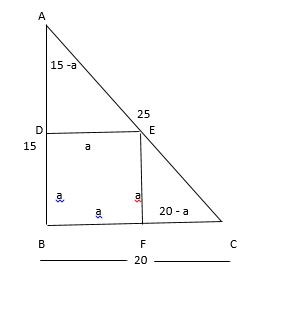Let the side of the square be a Then, AD = 15 – a and FC = 20 - a Area of Triangle ABC = 1/2 × Base × Height = 1/2 × 15 ×20 = 150 cm² Now, Area of Triangles ADE and EFC + Area of Square BDEF = Area of Triangle ABC ∴ 1/2 ×a × (15 - a) + 1/2 × a × (20 - a) + a² = 150 15a/2 - a²/2 + 10a - a²/2 + a² = 150 (15a+20a)/2 = 150 35a = 300 a = 300/35 = 60/7 cm Area of Square = 3600/49 cm²
Statement:Â
No musician is an architect.
All cricketers are musicians.
All players are architects.
Conclusion:Â
A certain number of people are sitting in a row, facing north. N is sitting third to the left of P. M is sitting third to the left of N. O is sitting th...
A number has been denoted to each of the given letters. Select the option from the following four possible arrangements of these numbers that forms a me...
In any code language, if MORTAL is coded as VSQPEX, what will be the code of GARDEN in that language?
Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it appears to be at variance...
In a certain code language, 'CODE' is coded as '1573' and 'DICE' is coded as '7185'. How is 'O' coded in the given language?
The figures given below show the sequence of folding a piece of paper and the method of cutting the folded paper. What will the paper look like when it ...
Which two mathematical signs should be interchanged to make the given equation correct?
15 × 3 ÷ 15 – (45 × 3) – 10 + (13 ÷ 2) = 76
...Select the letter-cluster from among the given options that can replace the question mark (?) in the following series.
DI, GO, LU, OA, TG, ?
Three of the following four letter-clusters are alike in a certain way and one is different. Pick the odd one out.
Relevant for Exams:
