Question
A vertical pole and a vertical tower are standing on the
same level ground. Height of the pole is 15 metres . From the top of the pole the angle of elevation of the top of the tower and angle of depression of the foot of the tower are 60° and 30° respectively. The height of the tower is:Solution
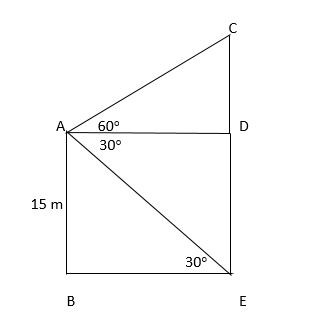AB = Pole CE = Tower AB = 15 m In ∆ABE tan30° = AB/BE 1/√3 = AB/BE 1/√3 = 15/BE BE = 15√3 m AD = BE = 15√3 In ∆ACD tan60° = CD/AD ⇒ √3 = CD/(15√3) ⇒ CD = 45 CD + DE = 45 + 15 ⇒ 60 m
Study the given diagram carefully. Which option correctly explains the reason for the appearance of the blue-black colour?
In India, if a religious sect/community is given “the status of a national minority, what special advantages is it entitled to?
1. It can estab...
First-ever national level Khelo India Women’s Hockey League (Under 21) inaugurated at which of the following Places in Dec 2021?
With reference to the Gross Domestic Product (GDP), select the correct statement from the option given below:
Bharani Festival also called Kodungalloor Bharani, is celebrated in which of the following states?Â
The concept of a Lambda Expression in functional programming is mainly used for:
Which languages are to be used for all or any of the official purposes of the State of Tripura as per the Tripura Official Languages Act, 1964?
Which one of the following is not an audio file format ?
Who is covered under the definition of "worker" under the Code on Industrial Relations, 2020?
Who among the following said, “The most perfect system of government is the one that produces the greatest possible happiness, the highest level of so...
Relevant for Exams:
