Question
The angle of elevation of the top of an unfinished tower at a point distant 78 m from its base is 30°. How much higher must the tower be raised (in
The angle of elevation of the top of an unfinished tower at a point distant 78 m from its base is 30°. How much higher must the tower be raised (in
m) so that the angle of elevation of the top of the finished tower at the same point will be 60°?
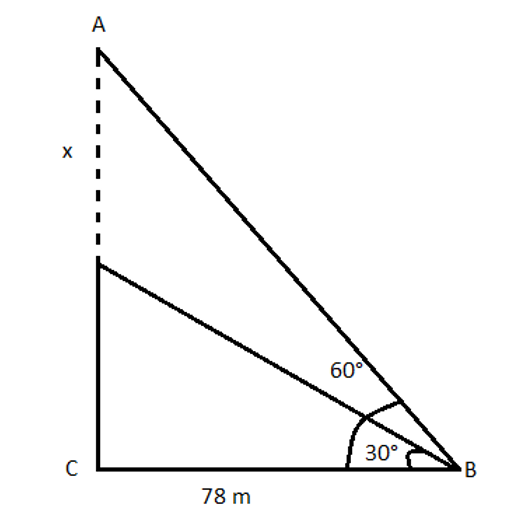Here, OC = Height of the unfinished tower AC = The height will be the finished tower's height In ΔOBC, tan 30° = OC/BC ⇒ 1/√3 = OC/78 [∵ tan 30° = 1/√3] ⇒ OC = 78/√3 ⇒ OC = (78 × √3)/(√3 × √3) = 26√3 .....(1) Let, the height of the tower will be raised (AO) = x In ΔABC, tan 60° = AC/BC ⇒ √3 = (OC + x)/78 [∵ tan 60° = √3] ⇒ x + OC = 78√3 ⇒ x + 26√3 = 78√3 ⇒ x = 78√3 - 26√3 = 52√3More Mensuration Questions
- The volume of a cube is 343 cm³. If the cost of painting the cube is Rs. 9 per cm², then find the cost of painting five faces of the cube.
- In the given figure, ABCD is a trapezium and AB!! DC. If OD = 3cm, OC = (x – 5) cm, OB = (3-x) cm and OA = (3x – 19) cm, then which Can the following be th...
- The length of a 744 metre long wire is 12 times the perimeter of a rectangular French garden. Find the area of the rectangular garden given that its length...
- In a rectangular floor of length and breadth of 20 metres and 10 metres, respectively, square tiles each of 2 metre edge length are to be laid. If the cost...
- The length, breadth and height of a storeroom are 17m, 10m and 12m respectively. If each box occupies 40 m3 of space, then how many boxes can be placed in ...
- A well with 20 m inside diameter is dug 10 m deep. Soil taken out of it has been evenly spread all around it to a width of 30 m to form an embankment. Find...
- A rectangular garden is bordered by a walkway of uniform width 5 metres. If the total area of the walkway is 1350 m², find the perimeter of the actual gard...
- The circumference of a circle is 110 cm and the length of the rectangle is 4 times the radius of the circle. Find the area (in cm2) of the rectangle, if th...
- Find the curved surface area of a cone whose height is 6 m and radius is 8 m. (in m 2 ) (approximate value) (The value of π is 22/7)
- The difference between the length and breadth of a rectangle is 25 m. If its perimeter is 206 m, then its area is
Relevant for Exams:
Hey! Ask a query
Please enter email id
The email must be a valid email address.
Please enter Mobile Number
Please enter valid Mobile Number
Please enter your Doubt
