Question
An equilateral triangle ABC is inscribed in a circle
with centre O. D is a point on the minor are BC and ∠ CBD = 40°. Find the measure of ∠ BCD.Solution
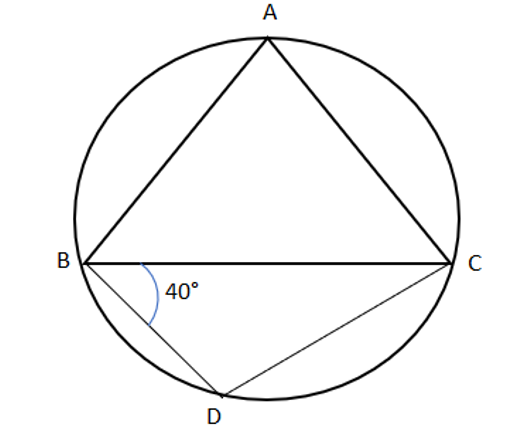∠ABC = ∠ACB = ∠BAC = 60° [∵ ΔABC is an equilateral triangle] Also, ∠BAC + ∠BDC = 180° ⇒ 60° + ∠BDC = 180° ⇒ ∠BDC = 180° - 60° = 120° Also, ∠CBD + ∠BDC + ∠BCD = 180° ⇒ 40° + 120° + ∠BCD = 180° ⇒ ∠BCD = 180° - 40° - 120° = 20° ∴ The value of ∠BCD is 20°
Two tangents are drawn from an external point to a circle with radius 8 cm, and the distance between the external point and the center of the circle is ...
A, B, and C together can do a work alone in 12 days, 18 days, and 54 days respectively. A alone starts the work and work for 3 days and leaves the work,...
A man invested a certain amount of sum at 12.5% per annum simple interest and earned an interest of Rs.3000 after 5 years. If the same amount is investe...
If Aman and Bhanu together earn Rs. ___ per month, and their incomes increase by 25% and 12.5% respectively, Bhanu's new income b...
A car travels 360 km in 4 hours. At the same speed, how far will it travel in 7 hours?
What is the average number of DELL laptops sold in all the given years?
The average weight of 32 dogs was initially computed to be 45 kg. However, it was later discovered that the weights of two dogs w...
Which of the following can create the largest printouts:
In triangle ABC, DE is parallel to BC. If AD = 3, DB = 2, and DE = 5, what is the length of BC?
Relevant for Exams:
