Question
What is the length (in cm) of chord PQ in a circle with a radius of 7 cm, where a diameter AB and non- diameter chord PQ intersect perpendicularly at point C, and the ratio of AC to BC is 4:3?
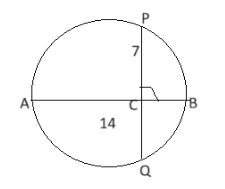Let AC = 4k and BC = 3k. Since C is the midpoint of AB (as AB is a diameter and C is where PQ perpendicularly intersects AB): AC + BC = AB Therefore, 4k + 3k = AB: 7k = AB Given AB = 2 × radius = 14 cm: 7k =14 k=2 Hence: AC =4k =4 × 2 = 8 cm, BC=3k=3×2=6cm PC = CQ (AB is the diameter of given circle and PQ is the perpendicular on AB) As we know, PC × CQ = AC × CB PC × PC = 8 × 6 PC2 = 48 PC = √48 PC = 4√3 Now, PQ = 2×PC PQ = 2 × 4√3 PQ = 8√3More Mensuration Questions
- Perimeter of a square shaped plot is 120 metres and the area of a rectangular plot is 65% more than that of the square shaped plot. Find the area (in m2) o...
- A hemisphere has a radius of 10 cm. What is the total surface area of the hemisphere?
- The side of a cube is 4m more than the side of a square. If the ratio of lateral surface area of the cube and the area of the square is 9:1, then what will...
- The length of a rectangle is 18 cm more than the side of a square. The perimeter of the square is 72 cm. If the breadth of the rectangle is 12 cm less than...
- The total cost of carpeting a rectangular floor at Rs 5 per sq.cm is Rs 1250. If the length of the floor is 25 cm, find its breadth.
- Determine the diameter of the incircle of a triangle where the semi-perimeter is 22 cm and the area is 66 cm².
- The area of the rectangular field is 600 m² and its perimeter is 100 m. Find how much percent less the breadth of the field is compared to the length of th...
- The lateral surface area of a cube is 484 cm2 . The length of a cuboid is 10% more than the side of the cube. The breadth of the cuboid is 9 cm less than i...
- Two paths of width 5 metres are to be made in the centre of rectangular field such that they are perpendicular to each other. Find the area (in m2) of the ...
- The radius of a cylinder is increased by 20%, and its height is decreased by 10%. Find the percentage change in the volume of the cylinder.
Relevant for Exams:
Hey! Ask a query
Please enter email id
The email must be a valid email address.
Please enter Mobile Number
Please enter valid Mobile Number
Please enter your Doubt
Think You're Ready for RBI Grade B?
RBI Grade B 2026 Phase 1 Memory Based Paper
- 200 Questions with Detailed Solutions
- Section-wise Coverage (GA, English, Quant & Reasoning)