Get Started with ixamBee
Start learning 50% faster. Sign in now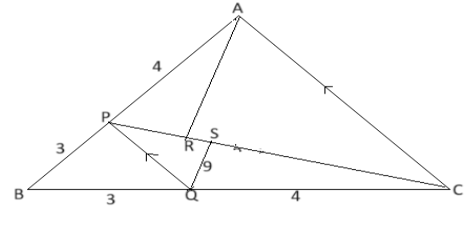
△ ABC with P on AB such that PB: AP = 3: 4. PQ || AC. AR ⊥ PC and QS ⊥ PC. QS = 9 cm. Proportional Segments: Given – PB: AP= 3: 4, let PB = 3k and AP = 4k. Therefore, AB = PB + AP=3k =4k = 7k. Similar Triangles: Since PQ || AC, triangles △ APQ and △ APC are similar. This implies the ratio of their corresponding sides is. PB/AB=3/7 Area of △PBQ/△ABC =9/49 Ratio of △APC and △QPC- =½ ×PC×AR: ½×PC×QS =AR: QS △APC/△QPC =AR/QS … (1) Area of △PBQ=9 and △QPC =12 Now Area of △APC =△ABC –(△PBQ+△QPC) =49-(9+12) =28. From Eq-(1) 28/12 =AR/9 AR =21cm.
A heavy rainfall warning has been issued in parts of Gujarat in the next few days due to a depression in the Arabian Sea which are likely to turn into a...
A moment delay (a) / would have proved costly (b) / in the situation. (c) / No error (d)
Even after all the corruption and mismanagement, the tribals of the North Eastern Region continue to send there children to study in government schools.
Yesterday, the Principal said that (A)/every students have to submit (B)/ articles for /(C) the school magazine. (D)
The following sentence has been divided into parts. One of them may contain an error. Select the part that contains the error from the given options.
In the sentence given below, four words have been printed in bold. One of these words may be misspelt or inappropriate in the context of the sentence. ...
Select the segment which has a grammatical error in the given sentence. If there is no error, select 'No error'.
When I go ...
The transition by online classes (A)/to offline education was smooth (B)/for the much part, (C)/ with teachers and students (D)/adapting at COVID-19 sa...
Change the given sentence into indirect form.
“What a nice man Mr Sharma is !” one of the guests at the party said.
As souls become aware that they (A)/ contain everything within themselves, they begin to (B) / comprehend and assimilate things needed for progress. (C)...
