Question
The secant CD intersects the circle at E and CF is
tangent to the circle at F. If the length of the secant CD is equal to 20 cm and the length of tangent CF is 15 cm, find the length of the chord DE.Solution
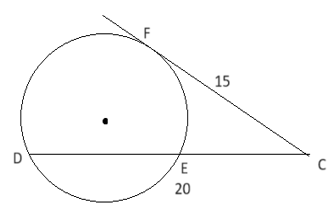CF is the tangent segment, which is 15 cm. CD is the secant segment, which is 20 cm. DE is the chord we want to find. According to the Power of a Point theorem: CF2 = CD × CE Since CD = CE + ED and CE =CD-DE, we can rewrite the equation as 152 = 20 × (20- DE) Now, 225 /20=20-DE 11.25 =20-DE DE =20-11.25 =8.75 The length of the chord DE is 8.75cm,
Statements:
Only a few Papers are Pencil.
No Pencil is Stapler.
All Staplers are Book.
Conclusions:
I) Some Book are not Pencil.
II) No Pencil is Book.
Statements: Some windows are door.
                         Some door are watch.
Conclusions: I. Some windows a...
Statements:
Some songs are guitars.
Only guitars are music.
No song is an instrument.
Conclusions:
I. Some...
Statement:
Only Asha is Jeenat
Some Asha are Charu
Some Charu are not Yash
Conclusion:
I. Some Yash are As...
In the question below there are three statements followed by two conclusions I and II. You have to take the three given statements to be true even if t...
- Read the given statements and conclusions carefully. Assuming that the information given in the statements is true, even if it app ear s to be at variance ...
Statements:
All present are past
 Some past are future
Only a few future is tense
Conclusions:
I. Some tense can ne...
Statement:
Only a few Heel is Sandal
All Sandals are Laces
Only Lace is buckle
Conclusion:
I. Some Heels are Lac...
- Statements:
Some machine are tool.
All tool are screw.
No screw is nut.
Some machine are ladder.
Conclusions:
<... Statements:
A few parrots are hens.
No parrot is bird.
All bird are sparrows.
Conclusions:
I: Some hens are not b...
Relevant for Exams:
