Question
The area of a rhombus is given as 384 cm², and its
perimeter measures 80 cm. Determine the total length of its two diagonals.Solution
Length of each side of the rhombus = 80 ÷ 4 = 20 cm
Let the length of longer diagonal be '2x' cm and that of smaller diagonal be '2y' cm.
So, (1/2) X 2x X 2y = 384
Or, xy = 192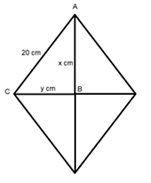 
Now, since the diagonals of a rhombus are perpendicular bisectors of each other. So, ABC is a right angled triangle.
And, in triangle ABC, we have
x2Â + y2Â = 400
Since, (x + y)2Â = x2Â + y2Â + 2xy
So, (x + y)2Â = 400 + 2 X 192
Or, (x + y)2Â = 784
So, x + y = 28
So, required sum = 28 X 2 = 56 cm
What is the Fully Accessible Route (FAR) introduced by the Reserve Bank of India?
Which of the following Article of the Constitution authorizes the Contingency Fund of India to facilitate meeting of urgent unforeseen expenditure by th...
During the financial year 2023-24, A had cash sales of ₹3,90,000 and credit sales of ₹1,60,000. His expenses for the year were ₹2,70,000, out of w...
A startup company with a promising technology but limited operating history and no substantial assets is seeking funding to fuel its growth and developm...
The concept of Corporate Social Responsibility (CSR) is based on which of the following theory?
Abnormal Gain is shown on the …….side of the Process A/c and the ………… side of Abnormal Gain A/c
Given the following information, calculate the Deferred Tax Asset (DTA) or Deferred Tax Liability (DTL) amount if the tax rate is 30%:
Profits as...
Under the IFSCA (Finance Company) Regulations, 2021, what activities qualify Finance Companies (FCs) and Finance Units (FUs) as Credit Institutions unde...
What do GFCs offer to importers, exporters, and other international trade participants?
In the revised instructions on foreign exchange risk hedging, what is the maximum exposure a user is allowed to take across all recognized stock exchan...
