Question
The length of three perpendicular distances of three
sides of an equilateral triangle from a point which lies inside that triangle are 9 cm, 8 cm and 7 cm respectively. What is the perimeter of the triangle?Solution
Let in ∆ABC, AB = BC = CA = a cm ON ⊥ AB OM ⊥ AC OP ⊥ BC Whose length respectively is ON = 9 cm, OM = 8 cm, OP = 7 cm. Area of ∆ABC = Area of ∆AOB + Area of ∆AOC + Area of ∆BOC √3/4 a² = 1/2 × ON × AB + 1/2 × OM × AC + 1/2 × OP × BC √3/4 a² = 1/2 × 9 × a + 1/2 × 8 × a + 1/2 × 7 × a √3/4 a² = 1/2a (9 + 8 + 7) √3/4 a² = 1/2 a × 24 √3/4 a² = 12 a a = (12 × 4)/√3 a = 4√3× 4 = 13√3 Side of ∆ABC, a = 16√3 ∴ Perimeter = 3 × 16√3 = 48√3
If ( p = 40 - q - r ) and ( pq + r(q + p) = 720 ), then find the value of ( p2 + q2 + r2).
If the ratio of the areas of two triangles is 4:3 and the ratio of their heights is 3:4, then the ratio of the lengths of their bases will be
- If x² - 2x + 1 = 0, then find the value of (x³ + x⁻³)(x + x⁻¹).
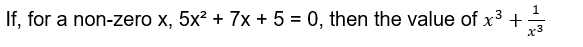
22% of ‘x’ is equal to 66% of ‘y’, then find the value of x: y.
If p = 36 - q - r and pq + r(q + p) = 310, then find the value of (p² + q² + r²).
- If p = 25 - q - r and pq + r(p + q) = 256, then find the value of (p² + q² + r²).
if √1+x/121 = 13/11 then find the value of x.
If (x 2 = 6x – 9), then find the value of [x³ + (x⁴/9)][5 - x³]
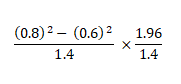
Relevant for Exams:


