Question
A container holds a mixture of milk and water, with milk
making up 60% of its contents. If 525 ml of the mixture is removed, and subsequently 50 ml of milk along with 128 ml of water is added, the new mixture results in the water being 33 ml more than the milk. Determine the original quantity of the mixture in the container.Solution
Let quantity of milk and water in the initial mixture be ‘3x’ ml and ‘2x’ ml respectively. Quantity of milk in 525 ml of mixture = 0.6 × 525 = 315 ml Quantity of water in 525 ml of mixture = 525 – 315 = 210 ml According to question; (3x – 315 + 50 + 33) = (2x – 210 + 128) Or, x = 150 Desired Answer = 5 × 150 = 750 ml
Evaluate:
7.5 + 12 ÷ (4 × 1.5) − 2.4
22% of 560 + 34% of 2160 × 5/12 =? + 16% of 920
(506 ÷ 22 + 9 × 3) × ? = 900 ÷ 9
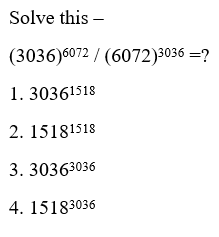
10³ = (? – 6) × 320 ÷ 8
7(3/6) of 534 + 262 = 61800 - ?
(150% of 950) ÷ ? = 25
181/8 + 51/4 – 63/8 = ? + 9/2
34 × 5 × 2 ÷ 6 + 7 × 5 + 13 = (?)× 6 – 754
What will come in the place of question mark (?) in the given expression?
?% of 2480 + 15 × 34 = 1440
Relevant for Exams:


