Question
If p and q are real numbers such that p2 + (p
- 2q - 1)2 = - 4q(p + q), then the value p - 2q isSolution
ATQ,
Let's solve the given equation step by step: Given: On Expanding the Equation (p−2q−1)2 , we get
Substituting back into the equation:
On Combine all p2 terms, we get:
Let Assume a simple relation:
Assume p - 2q = k (where k is a constant we need to find). Then = If k = 1, substitute p = 2q + k = 2q+1. Then, Substitute p=2q+1 into both sides: Simplify to verify if the equation holds true. Hence, it's shows that the equation is satisfied. therefore, The value of p − 2q is 1.
Find the maximum value of (20sin A + 15cos A).
if 7 sin 2 x + 2 cos 2 x = 4 then find tan x
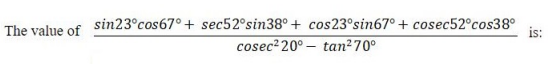
What is the simplified value of the given expression?
4(sin² 20° + sin² 70°) + 2sin 30° - (2sec 60° + cot 45°)
If cos²α + cos²β = 2, then the value of tan⁴α + sin⁸β is
If A lies in the first quadrant and 6 tan A = 5, then the value of 8 sin A−4 cos A / cos A+2 sin A is :
- If cosec [180° − (3q/2) ] = √2, 0° < q < 90°, then find the value of {(2/√3) X cos q - 4 cos 3q}.
Two buildings are 40 meters apart. The height of one building is 20 meters. From the top of the shorter building, the angle of elevation of the top of t...
- Find the value of sin²33° + sin²57° + cos²48° + cos²42°.
If 2cosθ + 8sin2θ = 11, where 0o < θ < 90o, then find the value of cot θ.
Relevant for Exams:


