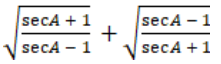📢 Too many exams? Don’t know which one suits you best? Book Your Free Expert 👉 call Now!
  • google app store apple app store
    • ✖

      Question

      R and S started a business with investments of Rs. ___

      and Rs. ___, respectively. After 4 months, X joined them with a capital of Rs. 24,000. After another 4 months, R withdrew all of her investment, whereas S invested Rs. 4,000 more. The ratio of the profit shares of S to X after 16 months of business was 11:9, while R's profit share was (3/19) th of the overall profit. The values given in which of the following options will fill the blanks in the same order to make the statement true:
      A 15,000 and 20,000 Correct Answer Incorrect Answer
      B 18,000 and 28,000 Correct Answer Incorrect Answer
      C 10,000 and 12,000 Correct Answer Incorrect Answer
      D 25,000 and 20,000 Correct Answer Incorrect Answer
      E None of these Correct Answer Incorrect Answer

      Solution

      ATQ, Let the investments of R and S be Rs. 'r' and Rs. 's' respectively. Ratio of the respective profit shares of 'R', 'S' and 'X' at the end of 16 months: = {r × 8}:{(s × 8) + (s + 4,000) × 8}:{24,000 × 12} = (8r) :(8s + 8s + 32,000) :(2,88,000) = (8r) :(16s + 32,000) :(2,88,000) = (r) :(2s + 4,000) :(36,000) ATQ: (2s + 4,000) :(36,000) = 11:9 So, 9 × (2s + 4,000) = 11 × 36,000 Or, 18s + 36,000 = 3,96,000 Or, 18s = 3,60,000 Or, 's' = 20,000 Now, Profit share of 'R' = (3/19) × {r + (2 × 20,000) + 4,000 + 36,000} So, 'r' = (3/19) × {r + 40,000 + 40,000} Or, 19r = 3 × (r + 80,000) Or, 19r = 3r + 2,40,000 Or, 16r = 2,40,000 Or, 'r' = 15,000 SO, 15,000 and 20,000 is correct pairs

      Practice Next
      More Partnership Questions

      Relevant for Exams:

      ask-question