Question
A shopkeeper purchased two rice bags, 'Brown Rice' and
'Basmati,' and sold them at identical prices. The bag of 'Brown Rice' was sold with a 20% profit, while the 'Basmati' bag was sold for a profit of Rs. 2925, resulting in an overall profit of 12.5% for the entire transaction. Given that the ratio of the cost price of 'Brown Rice' to that of 'Basmati' is 4:5, determine the cost price of the 'Brown Rice' bag.Solution
ATQ, Let, the cost price of Bag 'Brown rice' be Rs. '160x'. So, the cost price of Bag 'Basmati rice' = (5/4) × 160x = Rs. '200x' So, the selling price of Bag 'Basmati' = Rs. 200x + 2925 The total cost price of both the Bags = 160x + 200x = Rs. '360x' So, the total selling price of both the Rice bags = 1.125 × 360x = Rs. '405x' Selling price of Bag 'Brown rice' = 1.2 × 160x = Rs. '192x' So, the selling price of Bag 'Basmati rice' = 405x - 192x = 200x + 2925 Or, 213x - 200x = 2925 OR, 13x = 2925 Or, x = (2925/13) So, x = 225 Let, the cost price of Bag 'Brown rice' be Rs. '160x'. So, the cost price of Bag 'Basmati' = (5/4) × 160x = Rs. '200x' So, the selling price of Bag 'Basmati' = Rs. 200x + 2925 The total cost price of both the Bags = 160x + 200x = Rs. '360x' So, the total selling price of both the Bags = 1.125 × 360x = Rs. '405x' Selling price of Bag 'Brown rice' = 1.2 × 160x = Rs. '192x' So, the selling price of Bag 'Basmati' = 405x - 192x = 200x + 2925 Or, 213x - 200x = 2925 OR, 13x = 2925 Or, x = (2925/13) So, x = 225 The cost price of Bag 'Brown rice' = 160x = 160 × 225 = Rs.36,000
Three different positions of the same dice are shown. Select the letter that will be on the face opposite to the face having the letter 'F'?
Three different positions of the same dice are shown. Find the number on the face opposite the face showing ‘4’.
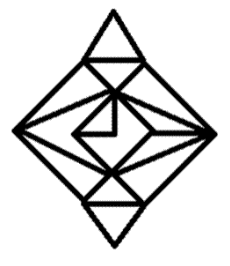
How many triangles are there in the given figure?
Select the dices which can be formed by folding the given sheet along the lines.
According to the given picture, 6 letters A, B, C, J, K and L are printed on each surface of the dice.
Which letter will be marked on the opposit...
Few cubes are arranged as shown in the figure. How many cubes are unseen?
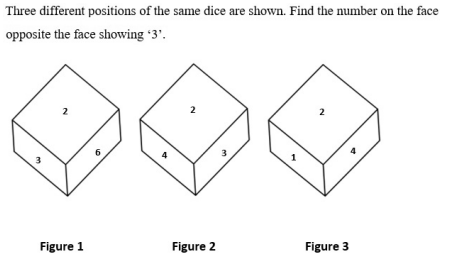
Study the following figures and find out the number opposite to 3.
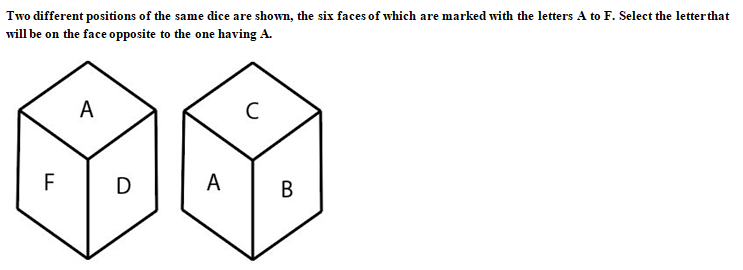
Four positions of dice are given below. Which letter will be opposite to D?
Relevant for Exams:



