Question
What will be the product of smaller roots of both
equations. Read the information given below and answer the following questions I. (a - 6)2 = (9a - P - a2) II. (P - b) 2 + (b + Q) 2 = 3(9b - Q) + 10 One root of equation 'I' is 2.5. Smaller root of equation II is (1/2) the larger root of equation I.Solution
For I: (a - 6)2 = (9a - P - a2) Or, a2 + 36 - 12a = 9a - P - a2 Or, 2a2- 21a + (36 + P) = 0 Since, 2.5 is a root of the given equation, 2 × (2.5)2- (21 × 2.5) + (36 + P) = 0 2 × 6.25 - 52.5 + 36 + P = 0 Or, 12.5 - 52.5 + 36 + P = 0 Or, - 40 + 36 + P = 0 So, 'P' = 4 So, the given equation becomes, 2a2- 21a + 36 + 4 = 0 Or, 2a2- 21a + 40 = 0 So, product of the roots = (40/2) = 20 So, other root of equation I = 20 ÷ 2.5 = 8 So, smaller root of equation II = 8 ÷ 2 = 4 Now, for II: (P - b)2 + (b + Q)2 = 3(9b - B) + 10 Or, (4 - b)2 + (b + Q)2 = 27b - 3Q + 10 Or, 16 + b2- 8b + b2 + Q2 + 2Qb = 27b - 3Q + 10 Or, 2b2- 8b + 2Qb - 27b + 6 + 3Q + Q2 = 0 Or, 2b2- b(8 - 2Q + 27) + 6 + 3Q + Q2 = 0 Since, 4 is a root of the given equation, 2 × (4)2 - 4 × (35 - 2Q) + 6 + 3Q + Q2 = 0 Or, (2 × 16) - 140 + 8Q + 6 + 3Q + Q2 = 0 Or, 32 - 140 + 11Q + 6 + Q2 = 0 Or, Q2 + 11Q - 102 = 0 Or, Q2 + 17Q - 6Q - 102 = 0 Or, Q(Q + 17) - 6(Q + 17) = 0 Or, (Q + 17) (Q - 6) = 0 So, 'Q' = 6, or 'Q' = -17 Required product = 2.5 × 4 = 10
Who heads the Monetary Policy committee formed by the Central Government?
In the context of a buffer in memory area or disk, spool refers to:
Which of the following books is an autobiography of the Indian politician LK Advani?
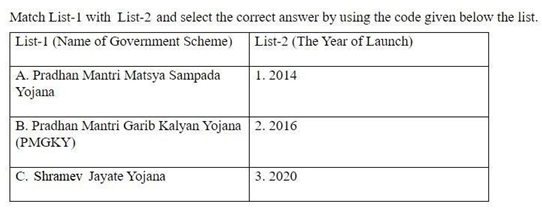
Harihara and Bukka established an independent state in Karnataka and established the capital city Vijayanagar on the banks of river _____________ in 1336.
In November 2020, ___________ has set a record of becoming the world’s fastest piano player ever.
Nobel Prize is announced at an international level which is administered by the Nobel Foundation in Stockholm, Sweden. Recently Nobel Prize winners for ...
Solve the following:
1800 ÷ (11 × 24 ÷ 8 × 3 – 69)²
What is the maximum age for a member of a joint public service commission to hold his/her office as per the Constitution of India?
The Third Battle of Panipat between the Marathas and Ahmad Shah Durrani , the ruler of Afghanistan was fought in the year:
Relevant for Exams:


