Question
If sin x + sin 2x = 1 and cos x + cos 2x = 0, find
x.Solution
Given sin x + sin 2x = 1 and cos x + cos 2x = 0. Using the double-angle identities: sin 2x = 2 sin x cos x and cos 2x = 2 cos² x - 1. Substitute sin 2x and cos 2x into the equations: From sin x + 2 sin x cos x = 1, sin x(1 + 2 cos x) = 1. (Equation 1) From cos x + (2 cos² x - 1) = 0, 2 cos² x + cos x - 1 = 0. Solving this quadratic equation gives cos x = 1/2 or cos x = -1. For cos x = 1/2, substitute into Equation 1: sin x(1 + 2 × 1/2) = 1, sin x(1 + 1) = 1, 2 sin x = 1, so sin x = 1/2. Thus, x = 30°. Answer: a) 30°.
Two students appeared in an exam and one secured 30 marks more than the other. If marks of the student who got more marks is 65% of the sum of the marks...
- Find the remainder when
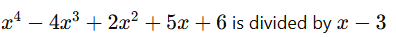
Find the range of the given data:
14, 28, 35, 21, 42, 56, 49
On dividing (5757 + 57) by 58, the remainder obtained is ‘R’. Find the value of (R – 5).
If the difference between two numbers is 52 and they are in the ratio 7 : 3, then find the greater of the two numbers.
When the digits of a two-digit number are interchanged, the new number becomes 8 less than 150% of the original number. If the sum of the digits is 7, f...
Sum of squares of three consecutive numbers is 770. Find the sum of first and third number.
A number 'N' when divided by 14 leaves 7 as remainder. If 5N² is divided by 14, then find the remainder.
The first number is four times 60% of the second number. If the second number is increased by 5, the first number becomes twice the new value of the sec...
Some pencils were distributed among (x + 2) students such that each student received 10 pencils. If there had been 5 students more, then pencils receive...



