Question
In this problem, you are presented with two quantities,
Quantity I and Quantity II.calculate both quantities and determine the correct relationship between them. Quantity I: Determine the number of factors of the number 20. Quantity II: If 'a%' of 200 is 8 more than 'b%' of 400, then find the value of (a - 2b). Now, compare Quantity I and Quantity II to establish the correct relationship between them and choose the appropriate option.Solution
ATQ, Quantity I: Factors of 20 = 1, 2, 4, 5, 10, and 20 So, number of factors of 20 = 6 So, Quantity I = 6 Quantity II: ATQ: (a/100) × 200 = (b/100) × 400 + 8 Or, 2a = 4b + 8 Or, a = 2b + 4 So, required value = 2b + 4 - 2b = 4 So, Quantity II = 4 So, Quantity I > Quantity II
Find the missing number.
.
...Choose the correct alternative that will complete the given number series. 2, 9, 28, 65, ?, 217
In the following question, select the missing number from the given alternatives.
45, 15, 60, 75, 135, ?
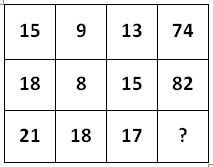
Study the given pattern carefully and select the number that can replace the question mark [?] in it.
Study the given pattern carefully and select the number that can replace the question mark [?] in it.
First row: 6, 5, 191
Second row: 9, ...
Select the number that can replace the question mark (?) in the following series.
Select the number from the given option that can replace the question mark (?) in the following series:
32, 16, 24, 60, ?, 945
Find the missing term :
...
Select the missing number from the given responses.
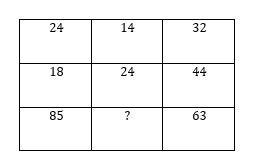
Find the missing term in the given series:
4 3.5 ? 22.875 ...


