Question
A man, after making the first investment, earned a total
interest of Rs. 1,09,200 at the end of 3 years. He invested a certain amount at an annual compound interest rate of 20%. At the same time, he invested another sum in two different parts in a scheme. In this scheme, he allocated 40% of the total amount to earn interest at a simple interest rate of (92/3)% per annum, while the remaining portion was invested at a simple interest rate of 20% per annum. Now, if the man had invested the entire amount in a simple interest scheme at a rate of 40% per annum for the same 3-year period, how much more interest would he have earned?Solution
Let the amount invested at compound interest be Rs. 'y' and the amount invested at simple interest be Rs. '5x' So, amount invested at (92/3)% p.a. simple interest = 5x X 0.4 = Rs. '2x' And, amount invested at 20% p.a. simple interest = 5x X 0.6 = Rs. '3x' ATQ; [{2x X (92/3) X 3}/100] + {(3x X 20 X 3)/100} + [y X {(1.2)3 - 1}] = 109200 Or, (46x/25) + (9x/5) + (0.728y) = 109200 Or, (46x + 45x) + 0.728y X 25 = 109200 X 25 Or, 91x + 18.2y = 109200 X 25 Or, 5x + y = 6000 X 25 So, 5x + y = 150000 So, interest the man would've earned had he invested the whole amount at 40% simple interest = {(150000 X 40 X 3)/100} = Rs. 1,80,000 So required profit = 180000 - 109200 = Rs. 70,800
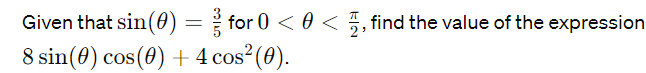
If
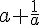 = -2 then find
= -2 then find 
Simplify:
6x + 8y - [(12x + 6y) - (4x + 3y) + 2y] - 4x1/3 + 1/15 + 1/35 + 1/63 + 1/99 = ?
189500 – 22650 + 48× ? – 352×18 = 162674
If (p/q) = (7/8) and (q/r) = (3/11), then the find the value of {(r – p)/(p + q)}.
- If, a 3 + b 3 = 485 and a + b = 5, then find the value of (1/a) + (1/b) .
If x = 21, then the value of x5 - 22x4 + 22x3 - 22x2 + 22x - 1 is
Relevant for Exams:


