Question
116 x (2/3)% of 420 + 666 x (2/3)% of 186 = 457 x (1/7)%
of 126 + 555 x (5/9)% of 198 + ? What will come in place of the question mark (?) in the following questions?Solution
Value of 100% = 1 116 x (2/3)% = 100% + 16 x (2/3)% = 1 + (1/6) = 7/6 666 x (2/3)% = 600% + 66 x (2/3)% = 6 + (2/3) = 20/3 457 x (1/7)% = 400% + 57 x (1/7)% = 4 + (4/7) = 32/7 555 x (5/9)% = 500% + 55 x (5/9)% = 5 + (5/9) = 50/9 Now, 116 x (2/3)% of 420 + 666 x (2/3)% of 186 = 457 x (1/7)% of 126 + 555 x (5/9)% of 198 + ? (7/6) × 420 + (20/3) × 186 = (32/7) × 126 + (50/9 )× 198+ ? 490 + 1240 = 576 + 1100 + ? ? = 54
(408 × 680)÷(20% of 680) = (250 × 260)÷ 10 + ? – 4500
If [8(x + y)3 – 27(x – y)3] ÷ (5y – x) = Ax2 + Bxy + Cy2, then the value of (A2 - 2B + 3C)...
- If [5a - (1/2a)] = 7, then find the value of [25a² + (1/4a²) - 3]
If
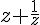= 2 then find If √b + (1/√b) = 11, then find the value of b + (1/b).
When positive numbers x, y and z are divided by 31, the remainders are 17, 24 and 27, respectively. When (4x - 2y + 3z) is divided by 31, the remainder ...
- If (x 2 = 8x - 16), then find the value of [x³ + (x⁴/16)][4 - x³]
- 42.5% of 20% of 960 = x + 18.4, then find the sum of the squares of each digit in 'x'.
If 125x3 - 64y3 = (Ax + By) (Dy2 - Cx2 + 20xy) , then the value of A + C - 2B + 3D is:
If 0.125x3 +0.216y3 = 210 and 0.25x2 + 0.36y2 = 10.30 then find the value of 0.5x + 0.6y.
Relevant for Exams:
