Start learning 50% faster. Sign in now
Within the realm of irrigation methods, when considering water use efficiency, which approach stands out as the most effective among the alternatives pr...
Dehradun-based Indian Institute of Petroleum has pilot tested to convert used cooking oil into:
Weeds propagating through tubers
Movement of leaves of sensitive plant, Mimosa pudica are due to
c
A preliminary scheme of agriculture typology for the better knowledge of the inherent agricultural characteristics and the tendencies in the changing sp...
Given below are two statements:
Statement I
Potassium is accumulated passively by both the cytosol and vacuole when extracellular K* co...
कौन सा सतत कृषि का घटक नहीं है?
The IFOAM is the worldwide umbrella organization for the organic agriculture movement, which represents close to 800 affiliates in 117 countries. What d...
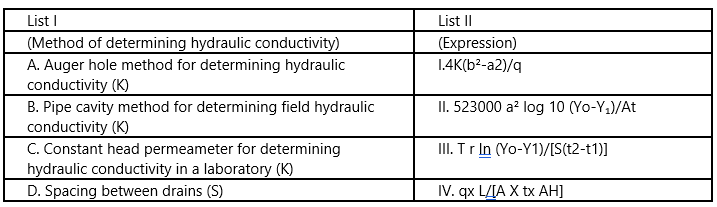
Match List I with List II