Question
1322 metres long train crosses a man who is moving in
the same direction with a certain speed, in 40 seconds. If the same train can cross a tree in 20 seconds with the same speed, then find the speed of the man.Solution
Speed of train = 1322/20 = 66.1 m/sec Let the speed of the man be ‘s’ m/sec Relative speed of the train = (66.1 – s) m/sec According to the question, (66.1 – s) = 1322/40 Or, s = 66.1 – 33.05 = 33.05 Therefore, speed of the man = 33.05 m/sec
If a = 2 + √3, then the value of (a6 + a4 + a2 + 1)/a3 is
If
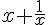 = 4 then
= 4 then (p + q) = 8 and (p2 + q2 - 6) = 28. If p < q, then determine the value of (p/q).
If √m + (1/√m) = 7, then find the value of m + (1/m).
if a2 + b2 + c2 = 2(3a -5b -6c)-70 , then a-b-c = ?
√(92×8 ×52+700) = ?
If p = 40 - q - r and pq + r(q + p) = 432, then find the value of (p² + q² + r²).
If p3 + 9p2 + 8p + 13 = 6p2 + 5p + 12, then find the value of {(p4 + 1/p2)}/(p2 + 3p +...
f(y) = y² – 5y + 6. Determine f(3) + f(–2).
If ( m+n ) : √ (mn) = 4, m>n , Then find the value of m : n ?
Relevant for Exams:



