Question
1200 metres long train crosses a man who is moving in
the same direction with a certain speed, in 30 seconds. If the same train can cross a tree in 20 seconds with the same speed, then find the speed of the man.Solution
Speed of train = 1200/20 = 60 m/sec Let the speed of the man be ‘s’ m/sec Relative speed of the train = (60 – s) m/sec According to the question, (60 – s) = 1200/30 Or, s = 60 – 40 = 20 Therefore, speed of the man = 20 m/sec
If a+1/a =9, then a5+1/a5 is equal to:
If a + (1/a) = 2, then find the value of (a5 + a3 + 6)/(7a – 5).
22% of ‘x’ is equal to 66% of ‘y’, then find the value of x: y.
If 3y-3/y=18 then find the value of y² +1/y²
If AB = x + 3, BC = 2x and AC = 4x − 5, then for what value of ‘x’ does B lie on AC?
Solve for x:
(2x − 1)/3 − (x − 4)/2 = 3
If √b + (1/√b) = 11, then find the value of b + (1/b).
If, 4x2 + y2 + 12x + 6y + 18 = 0, then find the value of (2x + y)/(y + 6x).
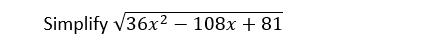
If ( p = 40 - q - r ) and ( pq + r(q + p) = 720 ), then find the value of ( p2 + q2 + r2).
Relevant for Exams:


