Question
8 men working 6 hours a day can complete a piece of work
in 6 days. If efficiency of each woman is 20% more than that of each man, then how many women working 4 hours a day are needed to complete the work in 12 days?Solution
Let the efficiency of each man be 'M' units/day. Let number of women required to complete the work in 12 days be 'N'. So, efficiency of each woman = '1.2M' units/day ATQ: We have, 8 X M X 6 X 6 = N X 1.2M X 4 X 12 Or, 288 = N X 57.6 So, 'N' = (288/57.6) = 5
More Time and work Questions
31% of 3300 +659 = ?
?= √(4 × ∛(16 × √(4 × ∛(16 ×…… ∝)) ) )
60% of 500 + (729) 1/3 - ? = 72
∛857375 + ∛91125 = ? + √6889
1365 ÷ 15 + (? ÷ 5) = 62 × 3.5
Find the Value of
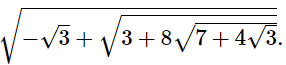
x= √(4 × ∛(16 × √(4 × ∛(16 ×…… ∝)) ) )
?2 = √20.25 × 10 + √16 + 32
36.76 + 2894.713 + 34965.11 =?
(2 ÷ 3) × (4 ÷ 12) × (? ÷ 10) × 45 × (1 ÷ 5) = (? ÷ 6) + (2 ÷ 5)
Relevant for Exams:
