Start learning 50% faster. Sign in now
Let the total work be represented as 1 unit. Work done by A per day = 1/15, Work done by B per day = 1/20, Work done by C per day = 1/30. In the first 3 days, A, B, and C work together: Work done in 3 days = 3 × (1/15 + 1/20 + 1/30) = 3 × (4/60 + 3/60 + 2/60) = 3 × 9/60 = 27/60 = 9/20 of the work. After 3 days, remaining work = 1 - 9/20 = 11/20 of the work. Now, B works alone for 5 days: Work done by B in 5 days = 5 × (1/20) = 5/20 = 1/4 of the work. Remaining work after 5 days = 11/20 - 1/4 = 11/20 - 5/20 = 6/20 = 3/10. In the next 1.5 days, B and D work together: Work done by B and D together in 6 days = 1.5 × (1/20 + 1/D) 1.5 × (1/20 + 1/D) = 3/10 1/20 + 1/D = 1/5 Work done by D per day = 3/20, Time taken by D to finish the entire work = 1 / (3/20) = 20/3 days.
Detemine the value of .
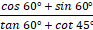
How many seats are there around the table?
. Radhika is 18th from the left end in a row of girls and Shivani is 20ththe from right end. Megha is 16th from Radhik...
किस संख्या का 18%संख्या 75 के 12%के बराबर है ?
John moves a distance of 8 km towards west. Then he moves towards south-east andcovers a distance of 6 km. From there, he moves towards east and travels...
Find which one of the given words cannot be made from the letters of the given word.
‘ FRIGHTMENT ’
...How many seats remain vacant in the row?
Which of the following is NOT an operating system?
Find which one of the given words cannot be made from the letters of the given word.
‘ TEMPERATURE ’
...