Question
A train approaches a tunnel a PQ. Inside the tunnel a
cat located at a point i.e., 7/16 of a distance PQ measured from the entrance P. When the train whistles, the cat runs. If the cat moves to the entrance of the tunnel P, the train catches the cat exactly at the entrance. If the cat moves to the exit Q, the train catches the cat at exactly the exit. The speed of the train is greater than the speed of the cat by what order?Solution
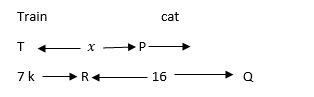Let the speed of train be ‘a’ and Speed of cat be ‘b’ and Train whistles at a point ‘T’, x km away from P, then First case: => a/b = x/(7k) Second case: => a/b = (x+16)/(9k) From both cases: => 9x = 7 (x+ 16 k) => 9x = 7x = 102 k => 2x = 102k => x/k = 56/1 => a/b = 56/(7x1) = 8/1
The average of 26 numbers is 45. If 4 is added to each number, then the new average will be:
- The profit earned on selling an item is 25%. If the cost price of the item was 20% less, and the selling price of the item was Rs. 30 more, then the profit...
{√676.12 + 13.012 – 146.89 } = ?
- Which of the following is not classified under the category of e-Banking?
‘A’ alone can complete a work in 30 days. ‘B’ alone can complete the same work in 40 days. If ‘A’ and ‘B’ work together for 6 days, then...
A man travels the first part of his journey at a speed of 40 km/h and the second part at a speed of 60 km/h. What is the average speed of the man?
A person who spends 55% of his salary saves the remainder. His salary goes up by 15%, but his savings stay the same, and he now spends Rs. 3,300 more. D...
A person is standing 30 meters away from the base of a building. If the angle of elevation from the person's eye level to the top of the building is 60 ...
In a 240 ml mixture containing milk and honey, honey makes up 56.25% of the total mixture. After removing 'p' ml of this mixture, 8 ml of honey is added...
Pawan, Qureshi, and Rittu can run 120 meters in 't' seconds, 't−2' seconds, and 't+3' seconds respectively. The speeds of Pawan and Rittu are in the r...
Relevant for Exams:
