Question
Train B which is ‘d’ meter long can cross a pole in
35 seconds. Train A can cross a platform of (d+10) meter long in (t+45) seconds. The ratio between the lengths of train A and B is 9:7 respectively. Train B can cross train A in (3t-70) seconds.If the difference between the speeds of both trains is 4 m/s, then find out the value of ‘t’.Solution
Let’s assume the speeds of train A and B are ‘Sa‘ and ‘Sb‘ respectively.
The ratio between the lengths of train A and B is 9:7 respectively.
Let’s assume the lengths of train A and B are 9y and 7y respectively.
Train B which is ‘d’ meter long can cross a pole in 35 seconds.
So d = 7y
7y = 35xSb
y = 5xSb Eq.(i)
Train A can cross a platform of (d+10) meter long in (t+45) seconds.
(7y+10) = (t+45)xSa Eq.(ii)
Train B can cross train A in (3t-70) seconds. If the difference between the speeds of both trains is 4 m/s.
(9y+7y)/(3t-70) = 4
16y = 4(3t-70)
4y =(3t-70) Eq.(iii)
In Eq.(i), Eq.(ii) and Eq.(iii), there are a total of four variables. We cannot determine the value of ‘t’ from the given information.

Select the correct mirror image of the given figure when the mirror is placed at MN as shown below.

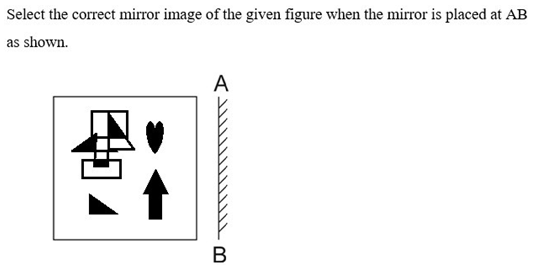
Select the correct mirror image of the given combination when the mirror is placed at line AB as shown.

Which of the answer figures is the exact mirror image of the given problem figure when the mirror is held at the right side?
If a mirror is placed on the line MN, then which of the answer figures is the right image of the given question figure?
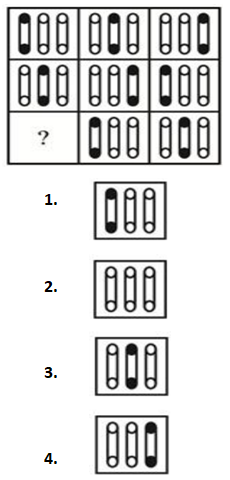
Which answer figure will complete the pattern in the question figure?