Start learning 50% faster. Sign in now
Let the speed of 'A' be 'x' m/sec.
ATQ,
{(180 + 100) /x} = 14
(280/x) = 14
So, 'x' = 20
So, speed of 'B' = 20 X 1.25 = 25 m/sec
Length of train 'B' = 180 X (5/6) = 150 metres
Required time = (150 + 100) /25 = 10 seconds
Approximately, the coefficient of variation for the given data where Pearson's second measure of skewness = 0.42, arithmetic mean- 86 and median 80, is:
Marshall-Edgeworth Index number:

For the distribution with unknown θ
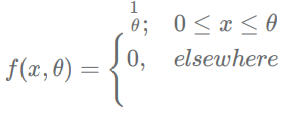
We set the tes...

For the frequency distribution of income (in lakh) of the employees in factory
Class 1.5-2.5 �...
A Poisson distribution has a double mode at x = 1 and x = 2. The probability for x = 1 or for x = 2 of these two values is:
At a round table, n persons are seated on n chairs. The probability that two friends from same college are sitting next to each other, is:
Statistics is not applicable to ________ observation.
For the following frequency distribution
Class : 3-5 5-7 7-9 ...