Question
In triangle ABC, the lengths of its sides are given as
AB = 8 cm, AC = 10 cm, and BC = 12 cm. Determine the length of the median drawn from vertex 'A' to the side BC.Solution
If ABC is a triangle such that AB = 'c', BC = 'a' and AC = 'b', then length of median from 'A': = √[(2b2 + 2c2 - a2) ÷ 4]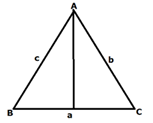 
Here, AB = 8 cm, AC = 10 cm and BC = 12 cm Therefore, required length of median = √[(2 X 102 + 2 X 82 - 122) ÷ 4] = √[(200 + 128 - 144) ÷ 4] = √(184/4) = √46 cm
The mass density of Kerosene is:
In an atom, which particles are responsible for chemical bonding?
From the given options, the speed of sound is highest in which material?
Which one of the following is the equation for Velocity Time relation?
Sounds of frequencies less than about ______ vibrations per second cannot be detected by the human ear.
Which law states that internal energy is a function of state and the increase in internal energy equals the sum of heat supplied to the system and work ...
Magnetic susceptibility of a diamagnetic material is:
Which of the following is the energy quantum of radiation?
What happens to the wavelength of light when it passes from a medium of higher refractive index to a medium of lower refractive index?
Which of the following statement is correct?
I. Value of ‘g’ is higher at poles than equator
II. Weight of an object at moon is 1...
