Question
In ∆ABC, AB = 5cm, BC = 6cm and AC = 10cm then find
out the value of cos A?Solution
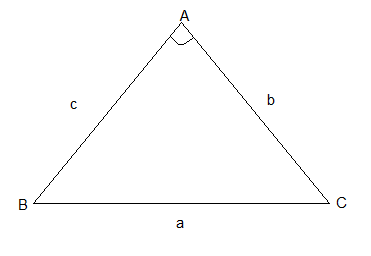From Cosine rule, we get BC2 = AB2 + AC2 - 2AB.AC.cos A 36=25+100-2×5×10×Cos A 100CosA=125-36=89 cos A = 89/100 .
Which of the following is not in the most powerful woman from India in the Forbes list 2023?
With reference to the Blue economy, consider the following statements:
1. Blue economy refers to the sustainable use of marine resources for expl...
Which rating agency predicts that by 2030, India will secure the position of the world's third-largest economy?
By FY28, Affordable Housing Finance Companies (AHFCs) are projected to have assets under management (AUM) of:
The Union Ministry of Culture is planning to revive the National Mission for Manuscripts (NMM) under which proposed autonomous body?
Recently Tamim Iqbal Announced Retirement from T20I Cricket . He plays from___?
India’s exports contracted by 1.15 per cent to _____________in August 2022?
Which of the following bank adjudged as best performing bank in Self Help Group (SHG) Linkage by Deendayal Antyodaya Yojana – National Rural Livel...
Who has become the first woman and African to head the International Olympic Committee?
In which Indian state is the fifth edition of Exercise Harimau Shakti-2025 with Malaysia being conducted?
Relevant for Exams:
