New Click here to Enroll in NaBFID Analyst Intro Class on May 6

    Question

    If 4sin² θ = 3(1+ cos θ), 0° <

    θ < 90°, then what is the value of (2tan θ + 4sinθ - secθ)?
    A 4√15-3 Correct Answer Incorrect Answer
    B 3√15-4 Correct Answer Incorrect Answer
    C 15√3+3 Correct Answer Incorrect Answer
    D 15√3-4 Correct Answer Incorrect Answer

    Solution

    4 (1 - cos2 θ) = 3 + 3cos θ ⇒ 4 - 4cos2 θ = 3 + 3cos θ ⇒ 4cos2 θ + 3cos θ - 1 = 0 ⇒ 4cos2 θ + 4cos θ - cos θ - 1 = 0 ⇒ 4cos θ (cos θ + 1) - 1 (cos θ + 1) = 0 ⇒ (4cos θ - 1) (cos θ + 1) = 0 ⇒ cos θ + 1 = 0 ⇒ cos θ = - 1 [Not possible because 0° < θ < 90] ⇒ 4cos θ - 1 = 0 ⇒ cos θ = 1/4 We can get all value by using the image below, 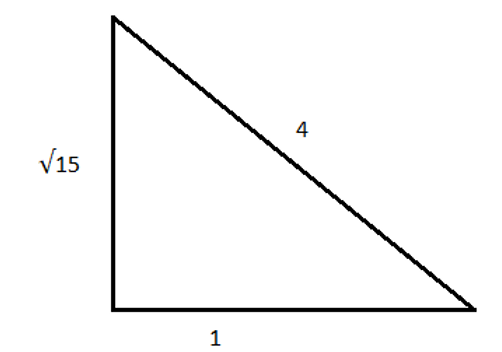The height will be = √(42 - 12) = √(16 - 1) = √15 So, (2tan θ + 4sin θ - sec θ) = (2 × √15) + (4 × √15/4) - 4 = 2√15 + √15 - 4 = 3√15 - 4

    Practice Next

    Relevant for Exams: