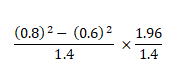Question
A ladder is leaning against a wall, making an angle of
60° with the ground. The top of the ladder reaches a window 15 meters above the ground. Find the length of the ladder, and also determine how far the base of the ladder is from the wall.Solution
Let the length of the ladder be L meters, and the base distance from the wall be d meters. From the triangle: sin 60° = Opposite/Hypotenuse = 15/L. √3/2 = 15/L. L = 15 × 2/√3 = 30/√3 = 10√3 m. cos 60° = Adjacent/Hypotenuse = d/L. 1/2 = d/(10√3). d = 15/√3 = 5√3 m. Correct answer: d) Length = 10√3 m, Distance = 5√3 m
If ( p = 40 - q - r ) and ( pq + r(q + p) = 720 ), then find the value of ( p2 + q2 + r2).
If the ratio of the areas of two triangles is 4:3 and the ratio of their heights is 3:4, then the ratio of the lengths of their bases will be
- If x² - 2x + 1 = 0, then find the value of (x³ + x⁻³)(x + x⁻¹).
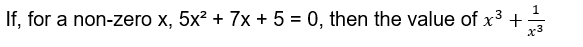
22% of ‘x’ is equal to 66% of ‘y’, then find the value of x: y.
If p = 36 - q - r and pq + r(q + p) = 310, then find the value of (p² + q² + r²).
- If p = 25 - q - r and pq + r(p + q) = 256, then find the value of (p² + q² + r²).
if √1+x/121 = 13/11 then find the value of x.
If (x 2 = 6x – 9), then find the value of [x³ + (x⁴/9)][5 - x³]