Question
The angle of depression of vertex of a regular hexagon lying in a horizontal plane, form the top of a tower of height 135 m located at the centre of the regular hexagon is 60°. What is the length of the each side of the hexagon?
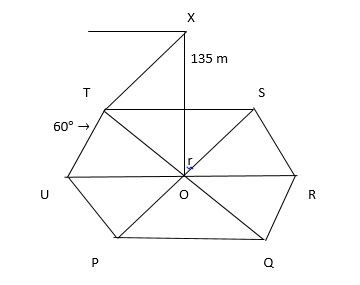Let OX be the height of the tower, angle of depression = Angle of elevation. y is the distance between u and o. In ∆XUO tan60° = 135/y √3 = 135/y y = 135/y ⇒ 45√3 In regular hexagon, ∆UOT, ∆ SOT,..... are equilateral triangles Length of hexagon = 45√3 mMore Trigonometry Questions
- Question 1
- If sin(A + B) = 1/2 and cos(A + 2B) = √3/2, where 0° < A, B < 90°, then find the value of tan(2A).
- Find the simplified value of the expression:sin 2 45 o + sin 2 60 o - (1/3) X tan 2 60 o - cos 2 60 o
- Question 4
- Simplify the given equation:
- If X = 15°, find the value of: sin²(3X) + cos²(4X) - tan²(2X)
- The angle of elevation of the top of a 70 feet tall tower from the initial position of a person on the ground was 30°. She walked towards the tower in a ma...
- Find the exact value of cos120°
- Simplify the following trigonometric expression: 15 cos 27° sec 63° − 9 cot 61° tan 29°
- (tan 5x - tan 3x - tan 2x) = ?
Hey! Ask a query
Please enter email id
The email must be a valid email address.
Please enter Mobile Number
Please enter valid Mobile Number
Please enter your Doubt
