Start learning 50% faster. Sign in now
At most two people celebrated their birthday after G. Neither F nor G celebrated their birthday on 28th of the month. The difference between the days of G and E to celebrate their birthday is 12. X celebrated his birthday immediately before E. No one celebrated their birthday between Y and F, who celebrated his birthday after Y. Z celebrated his birthday after H, who doesn’t celebrate his birthday before X. From above statements, Case-1 : Here G and E celebrated their birthday on 20th and 8th of the month respectively. X celebrated his birthday on 4th of the month. Y and F celebrated their birthday on 12th and 16th of the month respectively. Finally, H and Z celebrated their birthday on 24th and 28th of the month respectively. Thus all the given condition gets satisfied and we get the completed arrangement in Case- Case-2: Here G and E celebrated their birthday on 24th and 12th of the month respectively. X celebrated his birthday on 8th of the month. Y and F celebrated their birthday on 16th and 20th of the month respectively. As per last reference point, H doesn’t celebrate his birthday before X. Thus there is no other date left for H. Thus this case-2 becomes invalid and it can be eliminated.
24% of 400 × 16% of ? = 384
[{70 + (40 - 22) ÷ 3} ÷ 4] = ?
22 * 6 + 45% of 90 + 65% of 180 = ?
[(36 × 15 ÷ 96 + 19 ÷ 8) × 38] = ?% of 608
36×?² + (25% of 208 +13) = 60% of 2400 + 17×18
(360 - ?)/(25% of 96) = 13
Solve.
15.73 +13.25 +16.73 – 28.71 = 5 ×?
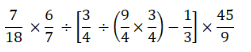
(11/12) × (18/22) × (4/3) + 3 = ?2