Question
Which of the following combinations is
true? Study the following information carefully and answer the given questions given below: Nine people P, Q, R, T, U, V, W, X and Y are living in a nine storey building .The ground floor is numbered 1 and the topmost floor is numbered 9. All of them like a different colour, viz Red, Green, Blue, Violet, Pink, Black, Purple, White and Yellow, but not necessarily in the same order. (i) Q likes Violet and lives on an even numbered floor. Y also lives on even numbered floor but he is not above the floor of Q. U lives on the second floor and likes Blue. (ii) The one who likes White lives on the fourth floor. The one who lives on the third floor likes Yellow. Y does not like White. (iii) There are two floors between the floors on which the persons who like Pink and Violet, live. (iv)There are three floors between the floors on which W and R live. W likes Green and R does not live on topmost floor. (v) T does not like Yellow and he does not live on the ground floor. (vi) There is one floor between the floor on which T and R live. V lives on a floor immediately above P’s floor. (vii) The one who lives on the topmost floor likes Red. There is only one floor between the ones who like Purple and Violet.Solution
From (i), it is clear that both Q and U are on even numbered floor and since, U is on 2nd floor, only 4th,6th and 8th floor are there for Q and Y. Since, Y is not above Q, there are two possibilities: Possibility (a) – Q at 8th and Y at 6th floor. Possibility (b) – Q at 6th and Y at 4th floor. But statement (ii) says, that one who likes white lives on 4th floor and Y does not like white, possibility (b) is not possible. Hence, we will go with possibility (a) which is Q at 8th (likes Violet) and Y at 6th floor. Statement (ii) also says that person on 3rd floors likes Yellow. From (iii), it is clear that the person who likes pink is on the 5th floor. From (vii), we can say that the person who likes red is on the 9th floor and also the person who likes purple lives on the 6th floor . From (v), T is not on the 1st floor and also since he does not like Yellow, he is not on the 3rd floor. 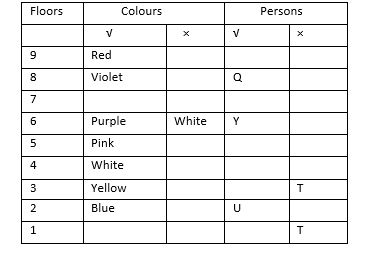 From (iv), neither W nor R can be at the 9th floor, as W likes green and R is not at the topmost floor. Also as W likes green, only two floors .i.e 7th and 1st, are left for W. Hence, there are two possibilities for W and R : Possibility (a) – W at 7th floor and R at 3rd floor. Possibility (b) - R at 5th floor and W at 1st floor. But we can see in the above table that T cannot be at 1st or 3rd floor. Now (vi), says that there is one floor between the floor on which T and R live. Hence, R also cannot be at 3rd floor. Therefore, possibility (a) cannot be correct. Hence, we will go ahead with the possibility (b) which is R at 5th and W at 1st floor and also from (vi), it is clear that T will be on the 7th floor. Only colourBlack is left for T, hence T likes Black. From (vi), it is also clear that V and P will be on 4th and 3rd floors respectively. Now only person left for 9th floor is X. Final arrangement will be as follows:
From (iv), neither W nor R can be at the 9th floor, as W likes green and R is not at the topmost floor. Also as W likes green, only two floors .i.e 7th and 1st, are left for W. Hence, there are two possibilities for W and R : Possibility (a) – W at 7th floor and R at 3rd floor. Possibility (b) - R at 5th floor and W at 1st floor. But we can see in the above table that T cannot be at 1st or 3rd floor. Now (vi), says that there is one floor between the floor on which T and R live. Hence, R also cannot be at 3rd floor. Therefore, possibility (a) cannot be correct. Hence, we will go ahead with the possibility (b) which is R at 5th and W at 1st floor and also from (vi), it is clear that T will be on the 7th floor. Only colourBlack is left for T, hence T likes Black. From (vi), it is also clear that V and P will be on 4th and 3rd floors respectively. Now only person left for 9th floor is X. Final arrangement will be as follows: 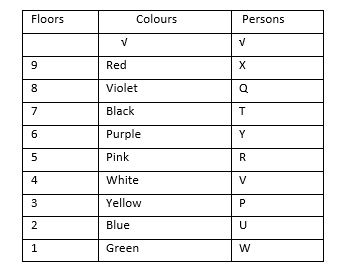
In the 4th edition of the Ranking of States on Support to Startup Ecosystems, which state was recognized as the "Best Performer" in Category B (States a...
How many number of Institutions are there in the Insurance Institute of India?
Which among the following Mughal Emperors propounded a new way of life/religion calledDin-i-Ilahi?
The statutory power for exchange control was provided to RBI by the Foreign ExchangeRegulation Act (FERA) of _.
Who was the winner of IPL 2022?
Gini coefficient is associated with which of the following measurements in an economy?
Consider the following statements & choose the correct options:
When two straight lines intersect then,
1. Adjacent angles are supplementa...
A bill providing for setting up of the Indian Institute of Petroleum and Energy in ______ was introduced in the Lok Sabha on July 18, 2017.
Which branch of physics deals with properties of fluids at rest?
What is the primary purpose of ISO 9001, the globally recognized standardization?
Relevant for Exams:


